Genetic Algorithms - An overview
Introduction - Structure of GAs - Crossover - Mutation - Fitness Factor - Challenges - Summary1. Introduction
For the not-quite-computer-literate reader: Genetic Algorithms (GAs) can be seen as a software tool that tries to find structure in data that might seem random, or to make a seemingly unsolvable problem more or less 'solvable'. GAs can be applied to domains about which there is insufficient knowledge or the size and/or complexity is too high for analytic solution (4). However, the previous sentence should not be read as 'areas of which we have no knowledge': such problems are often characterised by multiple and complex, sometimes even contradictory constraints, that must be all satisfied at the same time.
Examples are finding a best-fit solution, not necessarily the perfect solution, for crew and team planning, delivery itineraries, finding the most beneficial locations for stores or warehouses, building statistical models (5) and game playing behaviour (11).
So, what is different in GAs compared to more normal optimization and search procedures that it deserves interest? There are lots of reasons why:
- GAs work with a coding for the parameter set, not the parameters themselves.
- GAs search from a population of points, not a single point.
- GAs use payoff (objective function) information, not derivatives or other auxiliary knowledge.
- GAs use probabilistic transition rules, not deterministic rules.
- The Genetic Algorithms are first suited for the optimization problem.
- GAs are robust with respect to local minima, maxima.
- GAs work well on mixed discrete/continuous problems.
- GAs can operate on various representations.
- GAs are stochastic.
- GAs are easily parallelised.
- GAs are easy to implement and lend themselves well to hybridization.
- Sometimes there is simply no other approach.
However:
- GA implementation is still an art. They often require a lot of tweaking, then again sometimes you can tweak all you want and they will still find the same result.
- GAs are computationally expensive.
- GAs typically require less information about the problem (e.g. no gradients), but designing an objective function and getting the representation and operators right can be difficult.
Summarizing: it is suited for the dynamic program, because the genetic programming paradigm parallels nature in that it is a never-ending process. However, as a practical matter, a run of the genetic programming paradigm terminates when the 'termination criterion is satisfied' (16) ...
Therefore this page offers you some insight in what the GA is all about. Though it contains rather large and complicated mathematical formulas running in the background, I'll focus on what GAs do, their parameters and influence/effect of the components that make up genetic algorithms.
top of page
 back to IT stuff
back to IT stuff
2. Structure of GAs
GAs are categorised under the is an umbrella term Evolutionary Algorithms, which are used to describe computer-based problem solving systems which use computational models of evolutionary processes as key elements in their design and implementation. A variety of evolutionary algorithms have been proposed, of which the major ones are: GAs, evolutionary programming, evolution strategies, classifier systems, and genetic programming (check out www.google.com on these keywords). They all share a common conceptual base of simulating the 'evolution' of individual structures via processes of selection, mutation and reproduction. (11). But do not confuse these terms with their respective meaning in molecular biology! There is some resemblance, as you will see later on this page, but the researchers in informatics allowed themselves quite some liberties in modelling certain ideas of evolution. This does not mean it isn't possible from a theoretical point of view to adjust the algorithm to work with DNA as input data (see A GA for DNA?), but at the moment of writing this is certainly not the situation.
The existing GAs are founded upon the following main principles:
- Reproduction
- Fitness
- Crossover
- Mutation
There are various flavours of GAs in circulation, varying in implementation of these three parameters, but in essence the algorithms all follow a standard procedure:
- Start with a randomly generated population of n l-bit strings (candidate solutions to a problem). (These "solutions" are not to be confused with "answers" to the problem, think of them as possible characteristics that the system would employ in order to reach the answer (1))
- Calculate the fitness f(x) of each string in the population.
- Repeat the following steps until n new strings have been created:
- Select a pair of parent strings from the current population, the probability of selection being an increasing function of fitness. Selection is done "with replacement" meaning that the same string can be selected more than once to become a parent.
- With the crossover probability, cross over the pair at a randomly chosen point to form two new strings. If no crossover takes place, form two new strings that are exact copies of their respective parents.
- Mutate the two new strings at each locus with the mutation probability, and place the resulting strings in the new population.
- Replace the current population with the new population.
- Go to step 2.
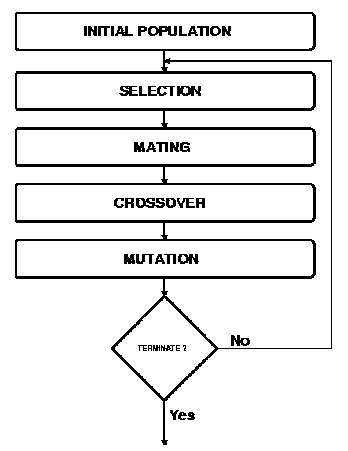
Figure 1. Simplified flow chart of a Genetic Algorithm (15).
This about the 'bird's eye view' of the structure of a genetic algorithm, the next two sections go into some detail about how above-mentioned principles are being used.
top of page
 back to IT stuff
back to IT stuff
3. Main parameters
The characteristics of the algorithm that have a major impact on the outcome when processing data with a GA are the implementation of crossover and the fitness factor. In contrast with molecular biology, mutation plays a secondary role.
3.1 Crossover
First, I'll briefly outline what crossover means form a biological viewpoint, and subsequently the two different ways it is implemented with GAs. During crossover, a random group (varying in size) of nucleotides of two lined up DNA strands are swapped (see Figure 2).

Figure 2. Crossover. The red and green lines are DNA strands
(which are strings of bits in a GA situation).
The algorithms code crossover as either a swap of one bit, which is more like a single-point mutation than a 'real crossover', or of several bits (used with genetic programming) and a distinction is made between two parents (bit strings, but called chromosomes in GA terminology) who are the identical, two different parents and single parent. Anyhow, the process has the following procedure:
- Select two bit strings (chromosomes), or in case of the genetic programming: select a branch of each parent.
- Cut the chromosome (or branch) at a particular location.
- Swap the bits/branches of the two parents. (15).
3.1.1 Single bit crossover
Some literature (3, 11, 12) work out the details of single point crossovers, and mention multiple bit crossover as part of 'genetic programming' but not as part of genetic algorithms. My interpretation of the literature I've read (see references) is that the original model devised by Holland, did use only single-point crossovers, i.e. instead of swapping a part of a bit string (similar to the DNA strand in Figure 2), only one bit is exchanged:111111 ------------> 111011 000000 crossover 000100and that this way of implementing crossover is still used nowadays.
A second way to implement single-bit crossover is to form a loop of the chromosome instead of lining up 2 strings to 'mate', because then the 1-point crossover can be seen as 2-point crossover with one of the cut points fixed at the start of the string. Thus 2-point crossover performs the same task as 1-point crossover, but it is more general. A chromosome viewed as a loop is able to contain more building blocks, as they are able to wrap around at the end of the string (13). Researchers now agree that 2-point crossover produces better results than 1-point crossover (6), though I have to admit I haven't read any form of proof and reasoning about that.
3.1.2 Multiple bits crossover
In line with previous two sections, the crossover operator exchanges sub-parts of two 'chromosomes' (read: bit strings), normally with a probability rate typically between 85% and 90% (12). The crossover operator randomly chooses a locus in the bit string and exchanges parts of the strings before and after that location to create two offspring. For example:the first string = 01001000
second string = 11101111 could be crossed over after the fifth bit (locus) in each to produce the two offspring:
01001111 and
11101000.
Here I chose the fifth location, but any integer position k along the string can be selected uniformly at random between 1 and the string length less one [1,l-1], which creates two new strings by swapping all characters between positions k+1 and l inclusively (16). See also Appendix B how genetic programming takes advantage of multiple crossover in a situation where the aim is to find a best-fit set of program instructions.
Last, I still need to find some more information on the Uniform Crossover; apparently each gene in the offspring is created by copying the corresponding gene from one of the parent chromosome, chosen according to a randomly generated crossover mask. Where a 1 exists in the crossover mask, the gene is copied from the first parent, and where a 0 exists in the mask the corresponding gene is copied from the second parent (13). More to come.
top of page
 back to IT stuff
back to IT stuff
3.2 Mutation
Crossover can generate a very large amount of different strings. However, depending on the initial population chosen, there may not be enough variety in the strings to ensure the GA covers the entire problem space. Or the GA may find itself converging on strings that are not quite close to the optimum it seeks due to a bad initial population. Some of these problems are overcome by introducing a mutation operator into the GA. The GA has a mutation probability, which dictates the frequency at which mutation occurs. Mutation can be performed either during selection or crossover. For each string element in each string in the mating pool, the GA checks to see if it should perform a mutation. If it should, it randomly changes the element value to a new one. In our binary strings, 1s are changed to 0s and 0s to 1s. (16, 12)
A text example:
original: he is an ignoranus
| |
mutant: she is an ignoramus
(2, adjusted)
The mutation probability should be kept very low (usually about 0.001%) as a high mutation rate will destroy fit strings and degenerate the GA algorithm into a random walk, with all the associated problems. But Tate and Smith (18) argue that the optimal mutation rates depend strongly on the choice of encoding, and that problems requiring non-binary encoding may benefit from mutation rates much higher than those generally used with binary encodings. The last word hasn't been said just yet about the relative importance compared to crossover and recombination (3, 11, 13).
Though (3) discusses the (ir)relevance of mutation, has tried to capture it in a mathematical model in context: let pm be the probability that a bit will be mutated, and that the function Sm(H) is the probability that the schema* H will survive the mutation. In order to survive the mutation, the schema must remain intact, therefore Sm(H) must be equal to the probability that a bit will NOT be mutated (1-pm) raised to the power of the number of defined bits in the schema, or:
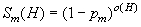
where o(H) is the number of defined bits (or order) of the schema and should be interpreted in the overall equation of a Schema Theorem* Holland devised:
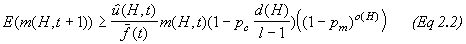 (3)
(3)See references 3 and 13 for more detail on the matter.
top of page
 back to IT stuff
back to IT stuff
3.3 Fitness factor
The name of this parameter has the resemblance of Darwinism, but only in the sense of the narrowed down phrase 'survival of the fittest', but some give it the more neutral name of selection operator. Setting the values of the fitness factor(s), in GA's context means assigning a value, its probability, to one or more strings as being a better solution than other strings that result from reproduction, crossover and mutation. But how to determine what is a better solution, i.e. to assign a higher probability rating? And should you define more than one factor affecting the fitness of a string, as is the situation in real life evolution?
This depends on the problem area.
- A situation with a known solution is the easiest one, because the final strings, or a close match is known and hence the factor, or factors, can be set accordingly. Shen (15) provides a simple example for optimising f(x)=x2 with strings of 5 bits. In text, one can imagine something like the following:
- Target solution: make
- 'made' is closer (in meaning) to make than for example 'lake' or 'sake' and further off is e.g. 'luke' with two failing letters; thus when a string 'made' occurs, it ought to have a higher survival rate than the others because it is closer to the solution. In this example I'll set the survival rate of made to 50%, or a probability of 0.5, and lake and sake to 20% each, leaving the luke fitness level at 10% (of course there are many more word options, but that's not important in this simple example).
- After setting the crossover and mutation values, you can decide on the randomly chosen input values, like hgfd, mfre, cvbn, mopa, which will go through the GA including the defined fitness factor, as shown in Figure 1 and Appendix A.
Another example could be improving compression/decompression software [algorithms] of images (where you discard and re-introduce information describing the picture): you know the final stage, and higher fitness levels could be assigned to intermediate pictures who have the composition of the picture roughly all right, but are blurred a bit, and lower values if the colours do not exactly match. So this means two types of fitness factors: the colour and the shape of a picture. Go figure with more complicated problems. - The situation where the intention is to find a solution. This focuses on devising the fitness function itself and testing with different values of the fitness function.
Determining the appropriate fitness function: With combinatorial optimization problems (more than one parameter) and where there are many constraints, most points in the search space often represent invalid chromosomes, hence having a zero "true" value. For a GA to operate successfully, a fitness function needs to be created where the fitness of an individual chromosome is seen in terms of how it is leading us towards valid chromosomes. This is in fact a sort of catch-22 situation, it should be known where the valid chromosomes are to ensure that the nearby points can also be given a good fitness values, and far away points given poor fitness values, but if it is not known where the valid chromosomes are this cannot be achieved. It has been suggested by Cramer (8) that if the goal of the problem is all or nothing, better results can be obtained if meaningful sub-goals are invented. These sub-goals should then be rewarded. Another approach which can been taken in this situation is to use a penalty function, which represents how poor the chromosome is and construct the fitness as (constant minus penalty) (10).
Determining values of fitness functions empirically: Every genotype, string to be tested will have a relative fitness assigned to it like mentioned under section 1 above. This is determined by a fitness function. The so-called fitness landscape is then constructed by assigning the fitness values of the genotypes to the corresponding points in the genotype space, using hamming code for example. This fitness value can be seen as a measure of how good a solution, represented by that point in the landscape, is to the given problem. Three things define this fitness landscape: A representation space (i.e. all the possible strings in the encoding), a neighbourhood relation denoting, which points in the representation space are neighbours, and finally a fitness function that assigns a fitness value to each point in the space (14). This results in nice graphs as if a blanket is spread over an uneven surface, where the peaks indicate better values of the parameters. To find out more on this on the web, search for the NK-model, which goes into more detail of the effect of the 'neighbours'.
top of page
 back to IT stuff
back to IT stuff
3.4 Other
As usual, more research is being carried out, not only related to the aforementioned three factors, but also the potential of incorporating more features of the real-live evolution. One technique is inversion (reversing the order of genes between two randomly chosen positions within the chromosome). Beasley et al. (6) describe inversion as mechanism by which the arrangement of the chromosome(s) may evolve instead of just swapping, known as karyotypic evolution in nature (13). But Syswerda (17) argues there is no need for inversion (7). I discussed adjustments to accommodate for the possibility of using real genetic sequences as input for GA computing here, and undoubtedly there will be more research and discussions on the matter of incorporating more, or better, parameters and characteristics.
4. Challenges
Referring to the long list of advantages in the introduction of this page the already used algorithms defining GAs, and proven use, it seems that a lot has been covered already, but this is not quite the situation, even though some, like (5), claim that "The genetic algorithm does not require any knowledge of how to get a solution for the problem to be solved; we only need a way to evaluate possible solutions". The first part of the quoted sentence sounds too good to be true: you don't have to know anything, just throw some data into a basket and it'll spit out what you would like to know. The troubles lie in the second part of the sentence, "we only need a way " Ahhh, what way? The outstanding issues can be divided into problems with the current technology and aspects of evolution that are not (yet) incorporated into evolutionary computing.
top of page
 back to IT stuff
back to IT stuff
4.1 Current technology
Representing the selection operators/fitness functions is not as easy as it may seem (see point 2 paragraph 3.4). Modelling fitness still appears to be an art with a high degree of trail-and-error.
Secondly, traditional GA's operating on fixed-length character strings. One reason that those binary linearly ordered representations are frequently used is that standard mutation and crossover operators can be applied in a problem independent way. (13). But not everything can be reduced to plain, simple and straightforward binary strings. Though other operators have been experimented with for various optimisation problems, thus far there haven't been widely adopted new general-purpose operators since GAs came about.
To what extend is a mutation of 1 per 1000 a good ratio? Would pointwise mutation alone suffice (9)? Is introducing mutation really the way to reduce convergence? Related to that: How does one recognize convergence and which evolutionary computations predictably converge (9)?
How do you define the 'ideal' amount to be crossed over? Maybe I haven't searched well enough, but I could not find data on the effect of differing crossover values, i.e. should one swap 1 bit during crossover as it was originally designed, or e.g. 10 or 100 bits? (9) Rightly puts into question if crossover is disruptive; if one doesn't know the 'correct' amount to be crossed over (would that even be possible to determine to a reasonable degree of informed guesstimate?). (13) Mentions that the crossover operator probability lies between 85% and 90%, which sounds like a high value of occurrence to me (from a biological point of view).
Nevertheless, problems like the Traveling Salesman Problem and finding workable rosters do show good results, suggesting that the used parameters and their values weren't too far off.
4.2 Open questions
Besides the list of questions already mentioned in the previous section, it is nice to look ahead at aspects that are not (yet) included in GAs. Following the analogy of real life genetics, what could be the roles of transposition, inversions and introns (9)?
Further, fitness levels are normally assigned to whole strings, but genes contain so-called conservative regions and genes that code for vital proteins in a DNA sequence, they ought not to change, or very rarely. If changes do occur in those sections, they 'must' lead to string death, i.e. failing the fitness test. To me, this sounds as potential candidates to define the fitness levels on, so ideally they should apply to parts of one string instead of a string as a whole as is it used to date.
Last, the way GAs are now used is to have input only at the start of running the program, but it would be nice if at some stage you could pause the program, introduce a group of new strings and then resume; a highly simplified way of modelling the effect of plasmids and certain viruses that incorporate themselves into DNA. Additionally, this might just be a way to reduce the problem of convergence.
top of page
 back to IT stuff
back to IT stuff
5. Summary
Genetic Algorithms can be applied to domains about which there is insufficient knowledge or the size and/or complexity is too high, or laborious, for analytic solution, for example making schedules or rosters and game theory. Characteristics involved are taken from genetics: crossover, mutation and fitness factors.
Crossover swaps a pre-defined amount of bits (usually 1 in GAs, but parts of code in the situation of genetic programming) from two strings of bits (called a chromosome), but this exercise can lead to convergence of the offspring instead of calculating towards a near-fit solution. Therefore, mutation is used, where one bit in a 1000 is set either from 0 to 1 or vice versa.
The fitness factor, also called the selection operator, is the probability that a given string (offspring) survives the generation and will be used for further calculations (crossover, mutation - the next generation of chromosomes). This factor, or factors, is set in advance and a string closer to a solution, if that is known, will be assigned a higher probability relative to others. The strings that do not match these criteria are 'killed', removed from the gene pool of possible solutions to the problem.
Though some good results are obtained with GAs, there is still much debate on the actual net effect and improvement of the parameters. Like, the amount being crossed over, its occurrence and the percentage of mutation. Defining fitness factors and determining the optimal values is another area of investigation. Last, one can draw further parallels with biological evolution and maybe implement more features into the computational models, think of assigning fitness levels to parts of strings (compare conservative regions in genes) or introducing a new set of input strings during the computation (plasmids, viruses).
top of page
 back to IT stuff
back to IT stuff
References
1. Anon. An Introduction to Genetic Algorithm and Genetic Programming. http://www.generation5.org/ga.shtml.
2. Anon. Genetic Algorithm. http://www.everything2.com/.
3. Anon. How Do Genetic Algorithms Work? http://www.generation5.org/ga_math.shtml.
4. Anon. Investigating the Performance of Parallel Genetic Algorithms. http://aquarius.solent.ac.uk/datrc/.
5. Anon. The genetic algorithm - brief description. http://www.pmsi.fr/gainita.htm.
6. Beasley, D., Bull, D.R. and Martin, R.R.. An overview of genetic algorithms part 1 fundamentals. Technical report, University of Purdue, 1993. (quoted in 13)
7. Beasley, D., Bull, D.R. and Martin, R.R.. Genetic algorithms, part 2 research topics. Technical report, University of Purdue, 1993. (quoted in 13)
8. C. N. L., J. Grefenstette, Ed.. A representation for the adaptive generation of simple sequential programs. In: Proceedings of the First International Conference on Genetic Algorithms, Lawrence Erlbaum Associates. 1985. pp 183-187. (quoted in 13)
9. Chen, Junghuei, Antipov, Eugene, Lemieux, Bertrand Cedeno, Walter and Harlan Wood, David. DNA Computing Implementing Genetic Algorithms. UDel_DIMACS_99.pdf, University of Delaware, Newark, DE, USA. 1999. 13 p.
10. Goldberg, D. E.. Genetic Algorithms in Search Optimization, and Machine Learning. Addison-Wesley, 1989. (quoted in 13)
11. Heitkoetter, J. and Beasley, D., Eds. The Hitch-Hiker's Guide to Evolutionary Computation: A list of Frequently Asked Questions (FAQ). USENET: comp.ai.genetic. rtfm.mit.edu:/pub/usenet/news.answers/ai-faq/genetic/. 1994. About 90 p.
12. Hill , Seamus and O' Riordan, Colm. Analysis of the performance of Genetic Algorithms and their Operators using Kauffman's NK Model. NUI-IT-100-102.pdf, Dept. of Information Technology, NUI, Galway, Ireland. 2002. 8p.
13. Hill , Seamus and O' Riordan, Colm. Genetic Algorithms, their operators and the NK-model. NUI-IT-150601.pdf, Dept. of Information Technology, NUI, Galway, Ireland. 2001. 11 p.
14. Hordijk, W.. A measure of landscapes. Technical report, Santa Fe Institute, 1995. (quoted in 13)
15. Shen, Jianjun. Genetic algorithms and genetic programming. GA-GP.pdf University Bielefeld, Germany. 2000. 27 p.
16. Shen, Jianjun. Genetic algorithms and genetic programming. GA-GP-text.pdf, University Bielefeld, Germany. 2000. 14 p.
17. Syswerda, G. Uniform crossover in genetic algorithms. In: Proceedings of the Third International Conference on article Genetic Algorithms, pages 2-9. Morgan Kauffmann, 1989. (quoted in 13)
18. Tate, D., David, M. and Smith, A.E.. Expected allele coverage and the role of mutation in genetic algorithms. Technical report, Dept. of Industrial Engineering, University of Pittsburgh, 1993. (quoted in 13)
top of page
 back to IT stuff
back to IT stuff
Appendix A
PSEUDO CODE
Algorithm EA is
// start with an initial time
t := 0;
// initialise a usually random population of individuals
initpopulation P (t);
// evaluate fitness of all initial individuals in population
evaluate P (t);
// test for termination criterion (time, fitness, etc.)
while not done do
// increase the time counter
t := t + 1;
// select sub-population for offspring production
P' := selectparents P (t);
// recombine the "genes" of selected parents
recombine P' (t);
// perturb the mated population stochastically
mutate P' (t);
// evaluate it's new fitness
evaluate P' (t);
// select the survivors from actual fitness
P := survive P,P' (t);
od
end EA.
(11)
top of page
 back to IT stuff
back to IT stuff
Appendix B
Mutation
- Only one function or term will be swapped for another function or term
- A complete sub-tree is replaced with another one.
Figure 3. Muatation in the situation of genetic programming;
left - Before, right - After (15)
Crossover Operation
- Chose the parents for a crossover operation
1) Probability: based on the Fitness of solutions
2) Selection: Fitness
3) Level of Fitness: Priority
An example with two parents:
( OR (OR D1 ( NOT D0 ) ) ( AND ( NOT D0 ) ( NOT D1 ) ) )
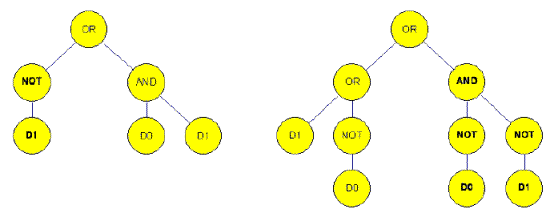
Figure 4a. Before crossover in the situation of genetic programming (15).
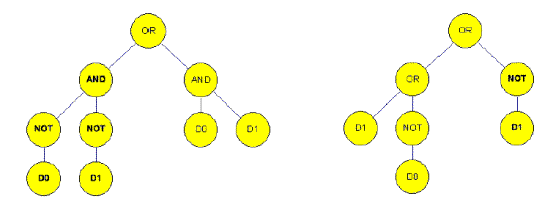
Figure 4b. After crossover in the situation of genetic programming (15)
top of page
 back to IT stuff
back to IT stuff
Appendix C
Schema stuff, ref 3, 12 and 13 - still to add -
 back to IT stuff
back to IT stuff